ИНЖЕНЕРНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК ПАРАМЕТРОВ СОСТОЯНИЯ

Числовые характеристики параметров состояния (мате­матические ожидания, дисперсии и др.), необходимые для расчета параметрической надежности, на этапе проектирования ЛА чаще неизвестны. Иногда невозможно установить их непосредственно по опытным данным и в период испытаний ЛА из-за невозможности прямого измерения параметров состояния. Поэтому возникает за­дача нахождения числовых характеристик распределения (в общем случае — закона распределения) параметра состояния по извест­ным числовым характеристикам (законам распределения) возму­щающих параметров, обусловливающих стохастический характер
функционирования рассматриваемого объекта (ЛА в целом или его отдельных бортовых систем, элементов корпуса и т. и.).

Решение такой задачи базируется на математической модели процесса функционирования объекта как динамической системы. За основу принимается детерминированная модель функционирования, используемая при проектировании объекта. Модель отображает преобразования случайных входных параметров (возмущений) в выходные параметры динамической системы (параметры состоя­ния).

Модели, соответствующие физическим процессам функциониро­вания конкретных узлов, агрегатов и систем ЛА, весьма разнооб­разны. Их разработка основывается на теоретической механике, аэродинамике, теории полета, теплотехнике, строительной механи­ке и ряде других дисциплин, но изложение специфических особен­ностей моделей не является целью данного учебного пособия. Огра­ничимся общей математической формулировкой модели функцио­нирования.

Модель функционирования как зависимость параметров состоя­ния Zv от возмущений Хі в достаточно общем виде представляет со­бой систему х обыкновенных дифференциальных уравнений перво­го порядка и (п—s) алгебраических уравнений связи:

dZ-tldt—F^Zs, Xh t);

<ly(Zv, Xl% 0=o,

где t= 1, 2, …, k v= 1, 2, …, и; /=1, 2, …, s; r=s+l, …, n.

Символы Fi и фг — известные функциональные зависимости. Возмущающие параметры Xt — случайные величины, в общем слу­чае коррелированные. К виду (1.72) удастся привести большин­ство моделей предварительными преобразованиями: понижением порядка производных, разрешением дифференциальных уравнений относительно производных, заменой ограничений типа неравенств, равенствами, сведением случайных функций к системе случайных величин. Последнее можно выполнить, например, методом канони­ческого разложения [13], согласно которому случайная функция

т

Г(*)=щ„(*)+2 Л>,(*), (1.73)

/ = 1

где mv(t)—математическое ожидание функции Y(t); Хі — некор­релированные центрированные случайные величины; срг-(/) —-неслу­чайные функции времени (координатные функции).

Иногда, например при определении надежности конструкции ЛА в условиях вибраций, целесообразно сохранить представление возмущающих воздействий в виде случайных процессов и восполь­зоваться в качестве модели передаточной функцией с применением преобразования Лапласа. Пусть выходной параметр Z(t) линейной динамической системы связан со входным возмущением X(t) диф­ференциальным уравнением

A{p)Z{t)=B{p)X{t (1.74)

где дифференциальные операторы:

A (p)=an/7n+an_i/7"-1+ … +ai/?+a0;

^(Р) = ^т/7’"+*т-іРт~І+ ■ ■ • ~Иі Р + Ь0; p=d/dt; (m<^.n).

Коэффициенты аг и Ьі в (1.75) —функции параметров динамиче­ской системы. Передаточная функция представляет собой отноше­ние изображений выходного и входного параметров [41]:

f-f [j. r.’j bm Ua’)m + bm — ] (j^)m 1 + … + bj (ум) + 6p

an (/“)” + an і (У01)” 1 + • ■ • + o-i (У“) — Ь o. q

Если X(/) —стационарный случайный процесс, то по спектральной плотности ЗЦсо) и передаточной функции нетрудно найти спект­ральную плотность выходного параметра (параметра состояния):

I (1.77)

Для нелинейных динамических систем и при существенных от­личиях законов распределения возмущений от нормального приме­няют другие стохастические методы [41].

Рассмотрим модель

dZ/dt=F{Z, Xі, t), (1.78)

предположив, что система имеет только один параметр состоя­ния Z.

Универсальным методом нахождения закона распределения f(z) параметра состояния по известным законам распределения fi(Xi) возмущений, пригодным практически для любых математи­ческих моделей, является метод статистического моделирования (метод статистических испытаний, или метод Монте-Карло).

Сущность статистического моделирования заключается в том, что зависимость (1.78) параметра состояния от возмущений реали­зуется многократно, всякий раз при новых, случайных значениях Х{. Полученные случайные значения параметра состояния подвер­гаются статистической обработке подобно результатам натурных испытаний объекта. Иначе говоря, на математической модели, как аналоге рассматриваемого объекта, многократно «проигрывается» стохастический процесс функционирования. Каждая операция за­дания путем случайного выбора значений возмущающих парамет­ров Х{, решения уравнения (1.78) и нахождения случайной реали­зации параметра Z(t), отвечающей этим возмущениям, называется пробой.

Статистическое моделирование основывается на формировании последовательности случайных чисел, подчиняющихся заданному закону распределения, причем исходным является равномерное рас­пределение в интервале [0, 1].

Для получения случайных чисел используют таблицы случайных чисел", генераторы случайных чисел и алгоритмы формирования псевдослучайных чисел на ЭЦВМ.

Таблицы случайных чисел применяют только при расчетах вруч­ную в связи с ограниченностью объема памяти ЭЦВМ.

В генераторах (датчиках) случайных чисел чаще всего исполь­зуют собственные шумы электронных ламп, преобразуемые в серию импульсов. Если к моменту опроса датчика имеющийся в нем счет­чик зафиксирует четное число импульсов, то это соответствует 1, в противном случае — это 0. Из нулей и единиц, выданных случай­ным образом датчиками, несложно получить далее случайные чис­ла, равномерно распределенные в интервале [0, 1].

Наиболее распространенным является метод псевдослучайных чисел, состоящий в том, что по специальным алгоритмаім на ЭЦВМ формируется неслучайная последовательность чисел, которые обла­дают статистическими свойствами независимых случайных чисел, имеющих равномерное распределение. Получение последовательно­сти таких псевдослучайных чисел представляет собой рекуррент­ный процесс: каждое последующее число образуется из одного или нескольких предыдущих путем несложных арифметических и ло­гических операций.

Алгоритмы формирования псевдослучайных чисел основаны на имитации хаотического перемешивания содержимого разрядов пра­вильной дроби, записанной в двоичном коде. Например, простей­ший алгоритм, предложенный Дж. Нейманом, так называемый метод середины квадратов, заключается в следующем. Произволь­ное число, состоящее из 2п двоичных цифр, возводится в квадрат. В результате, содержащем 4п цифр, отбрасываются по две цифры с обоих концов, остается «середина квадрата». Этот процесс повто­ряется многократно. Полученные «середины квадратов» представ­ляют собой последовательность равномерно распределенных в ин­тервале [0, 1] случайных чисел.

На практике применяются более сложные алгоритмы, дающие распределение лучшего качества. Так, в [22] рекомендуется проце­дура формирования. случайных чисел г,-, равномерно распределен­ных в интервале [0, 1], записываемая на языке Алгол-60 следующим образом:

procedure rav;

begin real г;

г : = и 1 м2; и1 : = и2;

if г > 4 then г: = г — 4;

ч’2 : = г;

rav: = /-/4;

end

Здесь rav -— идентификатор полученного случайного числа. Пе­ременные и и и2 описываются во внешнем блоке, им присваивают­ся начальные значения ы1: = 3,14159265; и2: =0,542101887. Много­кратное (циклическое) обращение к процедуре позволяет полу­чить последовательность равномерно распределенных случайных чисел.

2 1218

Числа, полученные на ЭЦВМ по специальным алгоритмам, стро­го говоря, не являются случайными, так как знание одного из них и рекуррентной зависимости позволяет однозначно определить все остальные числа. Ограниченность разрядной сетки ЭЦВМ не позво­ляет получить строгую равномерность распределения на данном интервале. Возможна повторяемость чисел с некоторой периодич­ностью. Поэтому обязательным этапом отработки алгоритма фор­мирования последовательности псевдослучайных чисел является статистическая проверка ее качества: случайности, непериодично — сти, равномерности.

С помощью случайных чисел г,, равномерно распределенных в интервале [О, 1], достаточно просто модулируют случайные qoбы­тия. Пусть Р(А)—заданная вероятность некоторого случайного события А. Появлению события А ставится в соответствие попада­ние случайного числа г, на отрезок числовой оси от 0 до Р(Л). Считается, что событие А имеет место, если п^Р(Л). При модели­ровании нескольких случайных событий Аи А2, Л3,… случайные числа Гі, г г-н, г,+2, … последовательности сопоставляются аналогич­ным образом с вероятностями каждого из событий.

Моделирование сложного случайного события заключается в моделировании составляющих его простых событий описанным вы­ше приемом и использовании теорем сложения и умножения ве­роятностей. Зависимые случайные события моделируют последова­тельно: сначала одно из них по безусловной вероятности его появ­ления, затем другое — по условной или безусловной вероятности в зависимости от результата моделирования первого события и т. д.

Реализация Хі некоторой случайной величины X, имеющей мате­матическое ожидание тх и среднее квадратическое отклонение ох, формируется при моделировании в виде

Х1 = тх+^х,

где — случайное число, позволяющее воспроизвести в серии проб заданный закон распределения случайной величины X; иначе гово­ря, |г есть реализация случайной величины подчиняющейся тому же заданному закону распределения, но с нулевым математическим ожиданием и единичной дисперсией.

На практике обычно требуется моделировать случайные величи­ны с отличными от равномерного законами распределения. Преоб­разование исходного равномерного в интервале {0, 1] распределе­ния в заданное с плотностью }(х) можно осуществить различными методами [11].

Метод нелинейного преобразования, обратного функции распре­деления, основан на свойстве интегральной функции распределе­ния, состоящем в том, что величина

(1.80)

распределена равномерно от 0 до 1. Решение уравнения (1.80) относительно х дает зависимость, преобразующую последователь­ность равномерно распределенных случайных чисел /у в последо­вательность случайных чисел Хь распределенных по закону f(x). Например, если f(x)—плотность экспоненциального распределе­ния (см. табл. 1 приложения), то

xt =—— — In г і. (1-81)

Аналогично можно моделировать распределение Релея:

Хі = о/~ — 2 In/у. (1-82)

Далеко не всегда удается получить решение уравнения (1.80) в элементарных функциях. Иногда для моделирования случайных величин используются специфические свойства законов распреде­ления. Так, моделирование нормального распределения основыва­ется на центральной предельной теореме, согласно которой сумма достаточно большого числа п случайных величин, равномерно рас­пределенных от 0 до 1, имеет распределение, близкое к нормально­му с математическим ожиданием я/2 и дисперсией н/12. В алгол — программе для моделирования нормального распределения случай­ной величины X с математическим ожиданием тх=0 и средним квадратическим отклонением 0зс=1 при п=12 можно использовать процедуру [22]: procedure norm; begin real s; integer i; s: = 0; for і: = 1 step L until 12 do s: = s + rav; norm : = s — 6 end

Здесь rav — идентификатор приведенной выше процедуры получе­ния равномерно распределенных от 0 до 1 случайных чисел.

Процедуры rav. и norm часто оформляются как стандартные подпрограммы. Используя их, можно моделировать другие распре­деления, например, с помощью следующей процедуры [22]: procedure у (ft, а, b, с, d, f, g, ft);

value к, a, b, с, d, f, g, h; integer ft; real a, b, c, d, f, g, ft; begin real si, s2; switch L : = l, 12, ІЗ, M;

.* 1 : rav; s2: = norm; go to L [ft];

l : у : = a X si + b; go to M;

/2 : у : = c + d X s2; go to M;

ІЗ : у : = sqrt ( — 2Х/Х/ХІП (sl>); go to M;

/ І: У : = ( — g X In (sl)) t (1/ft); go to M;

Л1 : end

Оператор, помеченный меткой /1, формирует равномерное рас­пределение в интервале [а, Ь] оператор с меткой 12 — нормальное распределение с математическим ожиданием с и средним квадра­тическим отклонением d, оператор с меткой 13 — распределение

2*

Релея с параметром f (1.82), оператор с меткой 14 — распределение Вейбулла с параметрами g и h.

Преобразование нормально распределенной случайной величи­ны X с математическим ожиданием тх и дисперсией ох2 в нормаль­но распределенную случайную величину У с параметрами ту и о,,2 выполняют при моделировании по зависимости

¥=tn„+(X — тх)(ау/ох). (1.83)

Для моделирования усеченного распределения (рис. 1.6) обыч­

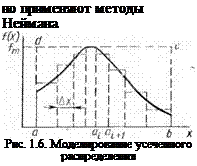или кусочной аппроксимации [11]. По методу Неймана из совокуп­ности равномерно распределен­ных в интервале [0, 1] случайных чисел Гі независимо выбирают па­ры чисел Ги ги преобразуют их в пары гн=а+{Ь — а)гн и т]2г = = /т-Г2г, где [й, Ъ] ИНТерВЭЛ ВОЗ­

МОЖНЫХ значений х, fm — макси­мальное значение плотности рас­пределения f(x). В качестве реа­лизаций моделируемой случайной величины принимают значения T]2i

начающсму, что соответствующие точки внутри прямоугольника abed лежат под кривой f{x). В справедливости такого приема не­трудно убедиться, поскольку вся площадь под кривой f(x) (см. рис. 1.6) равна единице, а вероятность попадания точки на этой площади в элементарную полоску с основанием Ах пропорциональ­на f(x). Метод Неймана обобщается и на случай формирования реализаций п-мерного случайного вектора с той лишь разницей, что. имитируют случайные точки не на плоскости, а в (п+1)-мер­ном объеме ПОД ц-мерной поверхностью f(xu Х2, …, хп).

Универсальным и сравнительно простым методом моделирова­ния распределений является метод кусочной аппроксимации, пред­ложенный Н. П. Бусленко. Сущность его при кусочной аппрокси­мации функции f(x) равномерным распределением состоит в следующем. Разобьем интервал [й, b] на т достаточно малых интер­валов [йг, йі+і], в пределах каждого из которых распределение мож­но считать равномерным (см. рис. 1.6). Пусть Р, — вероятность по­падания случайной величины X в интервал [йй,-+і]. Выберем дли­ны интервалов такими, чтобы вероятность попадания в них была одинаковой и равной 1 /т. Получим, как и ранее, пару случайных чисел rXi, г2ї из равномерного распределения [О, 1]; первое из них используем для случайного выбора г’-го интервала с вероятностью Pi как реализации случайного события, второе — для формирова­ния реализации моделируемой случайной величины: [4]

Для использования зависимости (1-84), являющейся рабочей,, не­обходимо иметь таблицу значений а,. Недостаток этого метода — неравномерная точность аппроксимации.

Для определения параметрической надежности важно уметь мо­делировать я-мерный случайный вектор Z параметров состояния из­делия, т. е. систему я коррелированных случайных величин Zb Z2, …. Zn. Для этой цели более приемлемым по сравнению с упомя­нутым выше моделированием многомерных распределений методом Неймана оказывается моделирование в рамках корреляционной теории методом линейного преобразования, сущность которого сво­дится к следующему. Заменим вектор Z о коррелированными со-

—>-

ставляющими вектором X с некоррелированными центрированными составляющими так, что

Zj — mZl Xj;

Zj = d2X j — j — X2,

Z3 ftiz,—CI31X1 “Ь #32-^2 Z3;

Zn — mzn=anlX1—an2Xi—… — ап, п-Х n_x— X n.

Элементы ciij матрицы преобразования и дисперсии а2х. найдем по заданным математическим ожиданиям mz. и корреляционной

матрице Ки вектора Z из условия некоррелированности случай­ных величин Xt:

M[XrXj]=0 при і Ф у; /= 1, 2…… я; }= 1, 2,…, я, (1.86) где М — символ математического ожидания.

Находя последовательно математические ожидания произведе­ний первого равенства (1.85) на второе, первого на третье, второго па третье и т. д., а также математические ожидания квадратов ра­венств (1.85) и используя условие (1.86), получаем зависимости для определения коэффициентов ац и дисперсий о*.:

ах1 — КIV —Кц1°хй °-tv—К. Ч 2 021ахъ

^31 = 7C3i/°jri; &32 = (^32 а2іаЗіаА-і)/°лг2; • ■ .

или в общем виде:

&і =:Кц1ахи t = 2,…, я;

&ij== (l/°ij) [Ки ■ airajr^r^ , j—2,…, і 1,

і—і

T-l

Таким образам, моделирование случайного вектора Z сводят к моделированию некоррелированных центрированных случайных’ величин Хі с дисперсиями и выполнению преобразования

(1.85).

Случайный процесс Z(t) моделируют аналогично многомерно­му случайному вектору, рассматривая фиксированные сечения ли­бо как коррелированные случайные величины, либо используя ка­ноническое разложение вида (1.73). При этом для стационарного случайного процесса наиболее простым является разложение в ряд Фурье, в котором роль координатных функций фг (t) играют три­гонометрические функции. Можно, наконец, вводить в модель опыт­ные реализации Zi(t), присвоив им номера и осуществляя случай­ный выбор очередной реализации с помощью равномерно распре­деленных случайных чисел. Более подробные сведения о технике статистического моделирования см. в [9], [11], [47].

Статистическое моделирование — универсальный метод, широ­ко используемый в расчетах надежности. Однако он обладает двумя недостатками. Первый заключается в больших затратах машиного времени, обусловленных необходимостью выполнения большого числа N проб (50-^500 и более), так как точность моде­лирования пропорциональна VN’, вторым является «слепота» ме­тода: в процессе моделирования не видно, как влияют возмущения на выходные параметры модели.

Поэтому наряду со статистическим моделированием на практике часто применяют различные приближенные методы, основанные на разложении интеграла уравнения (1-78) {в общем случае п пара­метров состояния — интегралов системы уравнений (1.72)] в сте­пенной или тригонометрический ряд по случайным возмущающим параметрам Хі, а в простейших случаях — метод линеаризации. Эти методы применимы, если не требуется найти закон распреде­ления параметра состояния Z, а достаточно определить его момен­ты (математическое ожидание mz, дисперсию а*)по известным моментам возмущающих параметров (тХг ах. и корреляционным моментам Кх;Х])-

Весьма эффективным с точки зрения экономии машинного вре­мени при приемлемой точности является метод эквивалентных воз­мущений, основанный на разложении решения уравнения (1.78)

Z=y(Xi, t), i=l, 2,…, k (1.88)

в ряд Маклорена по степеням центрированных возмущающих па-

О

раметров Х[=Х, — mx.. Ограничимся при разложении членами

ф-й степени:

q k k k

где

д1<е

дХ, … ах, *1 ^ 1

Индекс 0 указывает на то, что частные производные вычисляют­ся в точке {тх,, тХг,…, тХк]. Применяя к равенству (1.89) опе­рацию математического ожидания, получим

Q k_ k

тг=ч{тх., O + •••

ГТ і, "’і

о о

где р/,…/ =УИ [Л-*,.. .Л”/] — центральные моменты связи случай­ных величин Л’ц А2,…, А-*; / = 1, 2,…,^; iv…, it— 1, 2,…, k.

Идея метода заключается в том, что вычисление громоздких производных(t) заменяется суммированием с необходимыми весовыми коэффициентами |33- конкретных реализаций Zj(t) пара­метра состояния при реализациях gij случайных величин Х{ для каждой j-й пробы, выбранных определенным образом. Можно по­казать [30], что величины и gfj должны удовлетворять условиям

2 2 (1-90)

где Л/ — число реализаций, которое должно удовлетворять условию

а>—i-a+9- (1.91)

k+

Согласно методу эквивалентных, возмущений, вычисляют начальный момент р-го порядка случайной величины Z:

(1-92)

где 2,- — частное решение, т. е. результат j-й пробы, проведенной при определенной комбинации неслучайных величин являющих­ся специально выбранными реализациями случайных величин А (эквивалентными возмущениями).

Центральные моменты вычисляют по начальным. Решения Zj уравнения (1.78) представляют собой функции времени t, поэтому расчеты моментов необходимо проводить при фиксированных зна­чениях t.

Комбинации величин задаются так, чтобы часть коэффици­ентов рj обратилась в нули. Этим сокращается число необходимых интегрирований уравнения (1.78). Решение существенно упростит-

ся, если случайные величины Хі некоррелированы. При этом допу­щении, в простейшем случае <7=2, условия (1.90) имеют вид:

1 1; І РА?=0; І р$=<£; 1=1, 2,…, k-

Т (1.93)

2 її Ф hi ii ^2=1> 2,…, k.

j=і

Рекомендуется [30] проводить N=k+2 пробы, вводя значения І а в k пробах последовательно, по одному: в (&+1)-й пробе — все’ одновременно, в (&+2)-й пробе — также все одновременно, с об­ратными знаками. Система уравнений (1.93) имеет при этом сле­дующее решение:

У k; ру= l/k і= 1, 2,…, k; h+i=-H2k; %+2=l/2k.

Рассмотрим схему решения, предложенную для этого случая Б. Г. Доступовым [30]. Реализации возмущений удобно формиро­вать, полагая %1}==ас1}о^, где а — некоторый постоянный мно­

житель. Величины Сц принимают равными нулю или единице в порядке, указанном в табл. 1.2 для N=k+3 проб. Если положить <т=3, то становится ясным физический смысл этого параметра: ве­личина представляет собой в этом случае при нормальном рас­пределении предельное отклонение ДХі случайной величины Хі.

Таблица 1.2 і J 1 2 • • • k k+ k+2 A+3 1 1 0 0 1 —1 0 2 0 1 … 0 1 —1 0 — . . . • • • … • — • • . . • k 0 0 " * 1 1 —1 0

Очевидно, что (&+3)-я проба отображает нсвозмущенное функ­ционирование. На практике удобно задавать не средние квадрати­ческие отклонения °Xi возмущающих параметров, а коэффициен­ты вариации

Vxi—axjm хг ‘ (1.95)

В этом случае выражение (1.79) принимает вид *

■Xij=mXl(1 — faCijVXi) /== 1, 2,…, k j=, 2,…, /г + З. (1.96)

По результатам Zj(t), полученным при (£+3) пробах в фикси­рованных сечениях t—ta с выбранным шагом, рассчитывают мате­матическое ожидание параметра состояния:

* — >

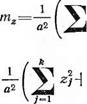I гк+2— gft+1

‘ 2

7-І 1

(1.98)

Нетрудно заметить, что при a-l^k эти выражения соответствуют рекомендациям (1.94).

Для решения задачи на ЭЦВМ с применением языка Алгол-60 можно рекомендовать следующую процедур"^: procedure dost; begin integer array с [1 : k, for і: = 1 step 1 until k do for j: = 1 step 1 until k do if і = j then c [i, j?]: = 1 else c [i, j]: = 0; for і: = 1 step 1 until k do begin j: = k 4- 1; c [/; j]: = 1;

jr: = ft 4- 2; c [i, J]: — — 1; j — = k +3; c [і, Д : =0;

end;

for j:= step 1 until k + 3do

begin for і: = 1 step 1 until k do

x [*‘> Л: = к[<]Х(1+вХс [і, j] X vx [/]); F;

end;

sum: = 0; for J : = 1 step 1 until k do sum : = sum + z [/];

mz — (sum + (z [k — f 2] — z [k + 1 ])/2)/(a Xa) +

г [ft + 3] x (1 — k/(aX e));

sum: = 0; for j: = 1 step 1 until ft do sum: = sum + (z [J]) f2;

sz: = sqrt {(sum + {(z [ft + 2])f2 — (z [ft + 1])| 2)/2)/(a X a)

+ (г [ft +3])t 2 X (l —k/(a X a)) — mz X mz);

end.

В процедуре приняты следующие индентификаторы: F — процеду­ра решения уравнения (1.78); mz и sz — математическое ожидание п среднее квадратическое отклонение параметра состояния Z; тхЩ и vx[i—математическое ожидание и коэффициент вариации возмущающего параметра Хі. Эти переменные, а также i, j, k, а, sum описываются во внешнем блоке.

Рассмотренный метод можно распространить и на общий слу­чай [модель (1.72)]. Метод эквивалентных возмущений не дает воз­можности найти закон распределения параметра состояния Z, но

зато позволяет выявить влияние, оказываемое на него каждым воз­мущающим параметром в отдельности. С увеличением степени. q аппроксимирующего полинома повышается точность, но одновре­менно растут и затраты машинного времени. Схемы расчета, даю­щие экономию, аналогичные табл. 1.2, для q—3 и <7 = 5 приведены в книге [30]. Метод эквивалентных возмущений оказывается более удобным при сравнительно небольшом числе возмущений.

Широко распространен на практике метод линеаризации (ме­тод малых возмущений), идея которого состоит в аппроксимации’ нелинейной в общем случае зависимости (1.88) линейной, статисти­чески эквивалентной исходной зависимости. Метод основан на до­пущении малости случайных отклонений возмущающих параметров Хі от их математических ожиданий гпх.. Он удобен, если зави­симость параметра состояния Z от возмущающих параметров Хі имеет явное однозначное аналитическое выражение

Z=?(Xe); /=1, 2,…, k (1.99)

при известных (обычно нормальных) законах распределения слу­чайных величин Хі.

Разложим функцию (1.99) и ряд Тейлора в окрестности точки («V, mXs,…, mXji) относительно центрированных возмущений, сохранив только линейные члены ряда:

тХг,…, ш, ) + 21 {ду/дхІ. (1.100)

к i~ 1

Индекс «т» при частных производных указывает на то, что их вычисляют в точке (mXt, mXs,…, mXjt). По теоремам о матема­тическом ожидании и дисперсии линейной функции

т2^т(т^, тХг,…, тх^ (1.101)

°’аі/ (іло2>

г /-1 і < і

где rXiXj — коэффициент корреляции величин Х{ И Xj.

Обозначение i<j указывает на то, что суммирование распро­страняется на все возможные парные сочетания величин Xt и Xj. Производные dq>/dXi представляют собой коэффициенты влияния возмущений Хі на параметр состояния Z. Если величины Хі и Xj некоррелированы (г*,.»^0) то в (1.102) сохраняется только пер­вая сумма под радикалом:

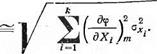(1.103)

Для упрощения следует по возможности так выбирать рассмат­риваемые возмущения, чтобы на основании каких-либо физических

соображений их можно было считать независимыми. Выражения­ми, аналогичными (1.103), можно представить коэффициент ва­риации vz или предельное отклонение Az параметра состояния, ис­пользуя соответственно коэффициенты вариации vх. или предель­ные отклонения Ахі возмущающих параметров.

При проектировании обычно бывают известны расчетные (сред­ние) значения Хі и возможные Предельные отклонения Ах І (допус­ки) возмущающих параметров. Их используют в расчете парамет­рической надежности: вместо математических ожиданий тх1

подставляют значения хі, а средние квадратические отклонения находят как

сх=Ах,/кіт, (1.104)

где k y—число средних квадратических отклонений, соответствую­щее вероятности у, с которой случайные отклонения, превышаю­щие Ахі, считают практически невозможными. Например, значению /ет=3 при нормальном распределении соответствует у=0,9973.

В частном случае зависимость (1.99) представляет собой про­изведение степенных функций некоррелированных возмущений:

к

Z— П Аг“‘- (1.105)

Г =»1

Логарифмирование и дифференцирование ее дает dZJdXi =

/ = 1, 2, …, k, на основании чего

= a*vlr (1.106)

“ «=1

Точность метода линеаризации зависит от степени нелинейно­сти функции (1.99) и малости отклонений возмущающих парамет­ров. В целях уточнения результата можно сохранить в разложении (1.100) члены порядка выше первого. В частности, при сохранении членов второго порядка, независимости и нормальном распределе­нии возмущений:

к

mz 3=: 9 (mXl, тх„-у ^ (д2<р/дХЇ)таІҐ (1.10 7)

/"і

Г і = 1 1—1 1/т I < у

(1.108)

Сопоставляя (1.101), (1.107) и (1.102), (1.108), можно оценить погрешность линеаризации.

1. Дайте определения безотказности, долговечности и ремонтопригодности изделия.

2. В чем заключаются различия между дефектом, неисправностью и отказом?

3. Дайте определения внезапных и параметрических отказов.

4. Чем обусловлено деление ЛА как сложной системы на элементы для расче­та надежности їв период проектирования?

5. Что является количественной характеристикой надежности элементов одно­разового срабатывания?

6. Перечислите количественные характеристики надежности невосстанавлива— емых элементов непрерывного функционирования.

7. Напишите зависимость вероятности безотказной работы от интенсивности отказов.

8. Какую интенсивность отказов элемента в режиме нормальной работы мож­но допустить, если его надежность в течение 1000 ч должна быть не ниже 0,95?

Ответ: Лг^5- 10~ь 1 /ч.

9. Как учитываются при определении надежности отличия условий и уровня нагрузки элементов от номинальных?

10. Что понимают под коэффициентом готовности?

11. Составьте структурную схему, надежности системы, условие безотказности которой сформулировано следующим образом: система безотказна, если безотказ­ны первый, второй и третий, а также четвертый или пятый элементы. Рассчитайте структурную надежность, полагая вероятность безотказной работы каждого эле­мента равной 0,9.

Ответ: 0,72171.

12. Дайте определение параметрической надежности и поясните его на при­мере одного ‘параметра состояния.

13. Давление на выходе газового редуктора имеет нормальное распределение с математическим ожиданием 5-Ю5 Н/м2 и средним квадратическим отклонени­ем 6,5-104 Н/м2. Падение давления ниже 3-10;> Н/м2 расценивается как отказ. Оп­ределите параметрическую надежность.

Ответ: 0,998965.

14. Параметры состояния Z[(t) и Z2(/), представляющие собой нормальные стационарные случайные процессы с нормированными корреляционными функция­ми р] (т) = е—0,4tcos 0,6т и Р2(т) = е—°’2” cos 0,8т, соответственно имеют оди­наковые математическое ожидание и дисперсию. Выброс какого из них за задан­ный предел R в течение фиксированного времени Т более вероятен?

Ответ: первого.

15. В чем заключается сущность статистического моделирования?

16. Используя зависимость (1.80), получите выражение для преобразования последовательности равномерно распределенных от 0 до 1 случайных чисел г» в последовательность случайных чисел Хі, имеющих распределение Вейбулла.

т.—————

Ответ х, = у — х0 In r-t.

17. В чем заключается сущность метода эквивалентных возмущений? Какие преимущества и недостатки имеет этот метод по сравнению с методом статисти­ческого моделироваиия?

18. Охарактеризуйте область применения метода линеаризации в расчетах параметрической надежности.